Sončna usmerjenost (koncentracija) s paraboličnim sončnim sprejemnikom

Parabolična geometrija je podlaga za koncentrirano tehnologijo sončne energije (CSP), kot so solarna korita in priprava jedi v sončnih pečeh. Sončni sprejemniki s paraboličnim koritom se štejejo za eno najbolj zrelih in najbolj komercialno dokazanih tehnologij v objektih CSP, zato je treba o tej vrsti podrobneje preučiti vsa fizikalna načela vključno s koncentrirano sončno energijo.

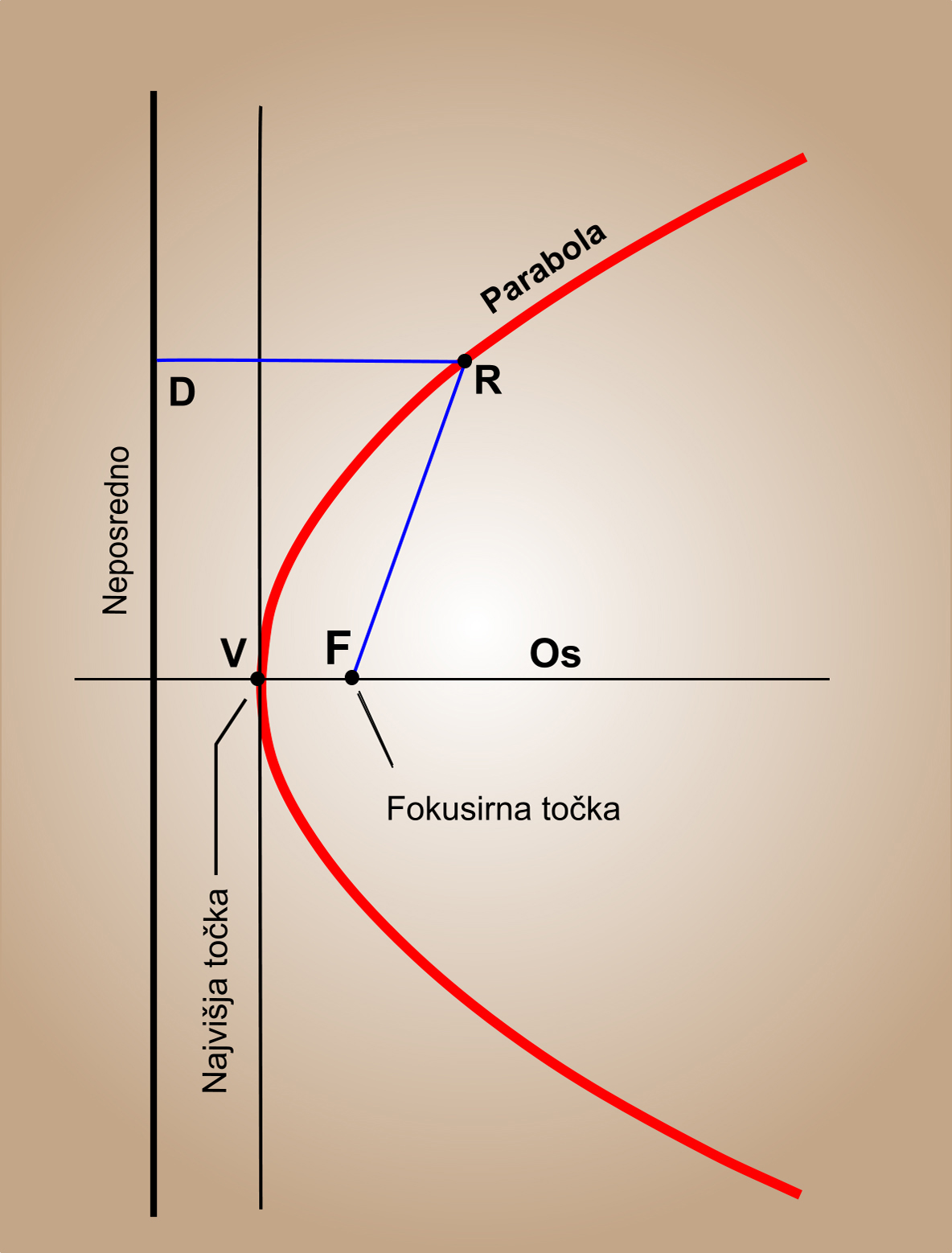
Parabola je množica točk, ki ležijo na enaki razdalji neposredno od točke x in so osredotočene s poudarkom na osrednjo točko, kot je prikazano na sliki 1. Za vsako točko DR = FR, ki je razdalja parabole med vozliščem VF in osjo ter je goriščna razdalja (f). Linija, pravokotna na smernico, ki poteka skozi točko F, je os parabole. Os deli parabolo na dva dela, ki sta simetrična.

S poudarkom na vrhu in osi parabole, vzeta kot x-os, se parabola izpiše z enačbo:

y² = 4 fx, kjer je f goriščna dolžina.

Po definiciji žariščne točke se v paraboli vsi prizori, ki so vzporedni z osjo parabole, odražajo skozi središče. Za omogočanje možnosti za svetlobno koncentracijo se uporabijo parabolične površine. Če predpostavimo, da sončna svetloba prispe na površino kot v bistvu vzporedni žarki, uporabimo odsevanje, ki je enako kot pri vpadnem kotu, ter tako določimo kontaktno točko kot idealno točko za sprejemnik (slika št. 2).

Solarni namenski programi obravnavajo parabolo s končno višino (slika št. 3). Zasnova paraboličnega reflektorja upošteva razpoložljivo velikostjo zaslonke (a), fokusno mesto (f , na primer, kjer bi bil sprejemnik nameščen) in višino reflektorja (h). Ti parametri so medsebojno povezani z

enačbo:

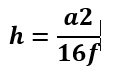
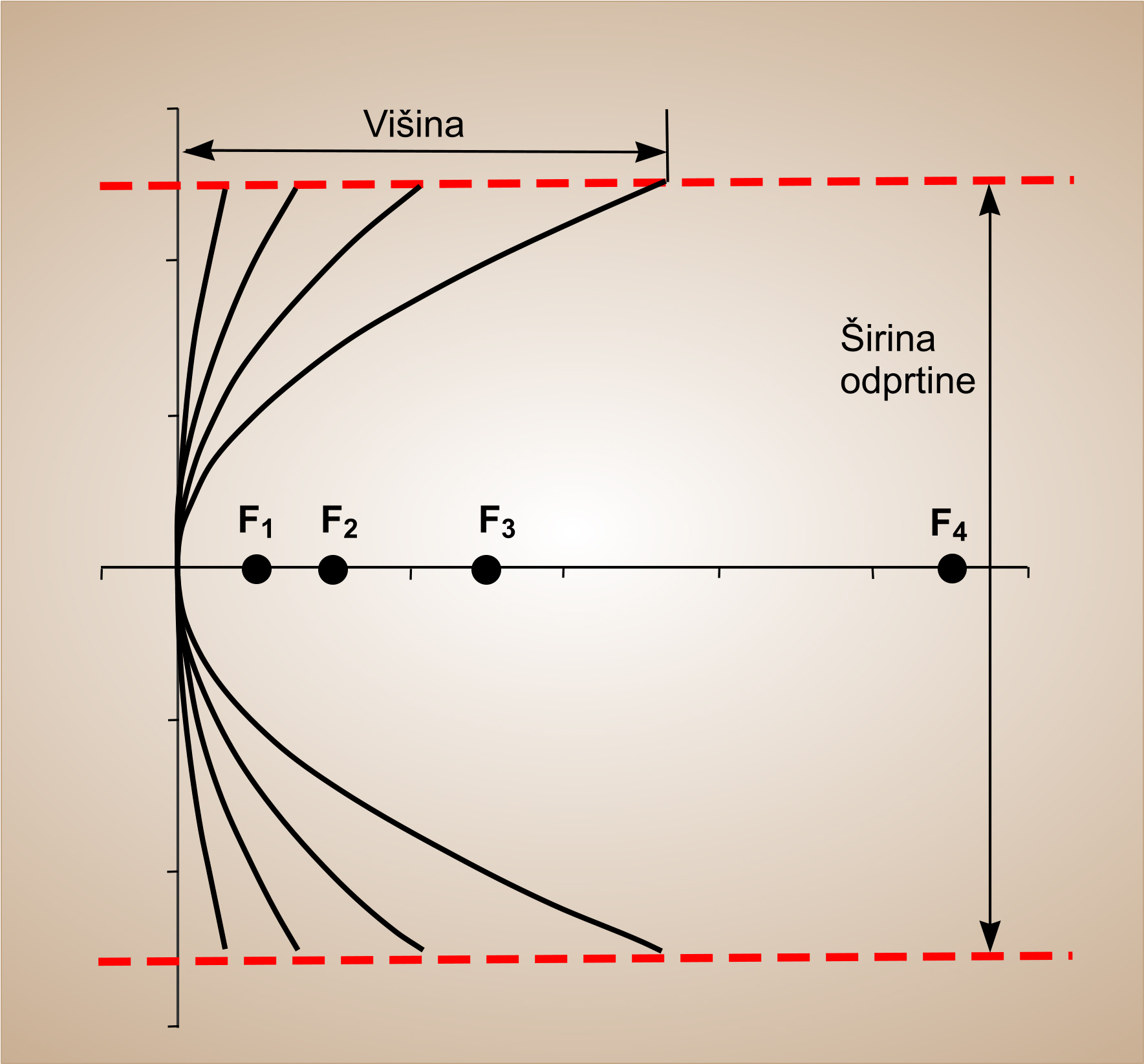
Ta slika zgoraj kaže, da je površina, ki se odbije, večja od glavne dolžine. Za "ravnost" oblike končne parabole je značilen kot (ф). Ko se ta kot za površine povečuje (znotraj iste odprtine), postane parabola bolj ukrivljena v žariščni razdalji in se skrajša.

Parabolična korita (slika 4) so tipičen primer koncentracije za preslikovanje, ki uporabljajo geometrijska razmerja, o katerih smo govorili zgoraj. Parabolično korito je ena od najbolj razširjenih tehnologij za koncentracijo sončne svetlobe na lestvici koristnosti. Ta vrsta zbiralcev se opira na sledenje soncu, da se zagotovi sevanje žarkov, ki so usmerjeni vzporedno s parabolično osjo.

Parabolično zrcalo ustvarja sliko o soncu na površini sprejemnika, zato je treba velikost sprejemnika ujemati z velikostjo slike. Ker sonce ni res točkovni vir, je sončni žarek na reflektorju predstavljen kot stožec s kotno širino 0,53^o (zato je pol kot med stožčasto osjo in njeno stranjo 0,267^o). Če se odraža v točki na parabolični površini, žarek zadene goriščno ravnino, kjer proizvaja sliko določene dimenzije, ki je osredotočena na žarišče. Premer cilindričnega sprejemnika (D), ki bi prestregel celotno odbito sliko, se lahko teoretično izračuna s širino odprtine (a) in kotom (ф), kot sledi:

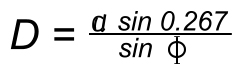
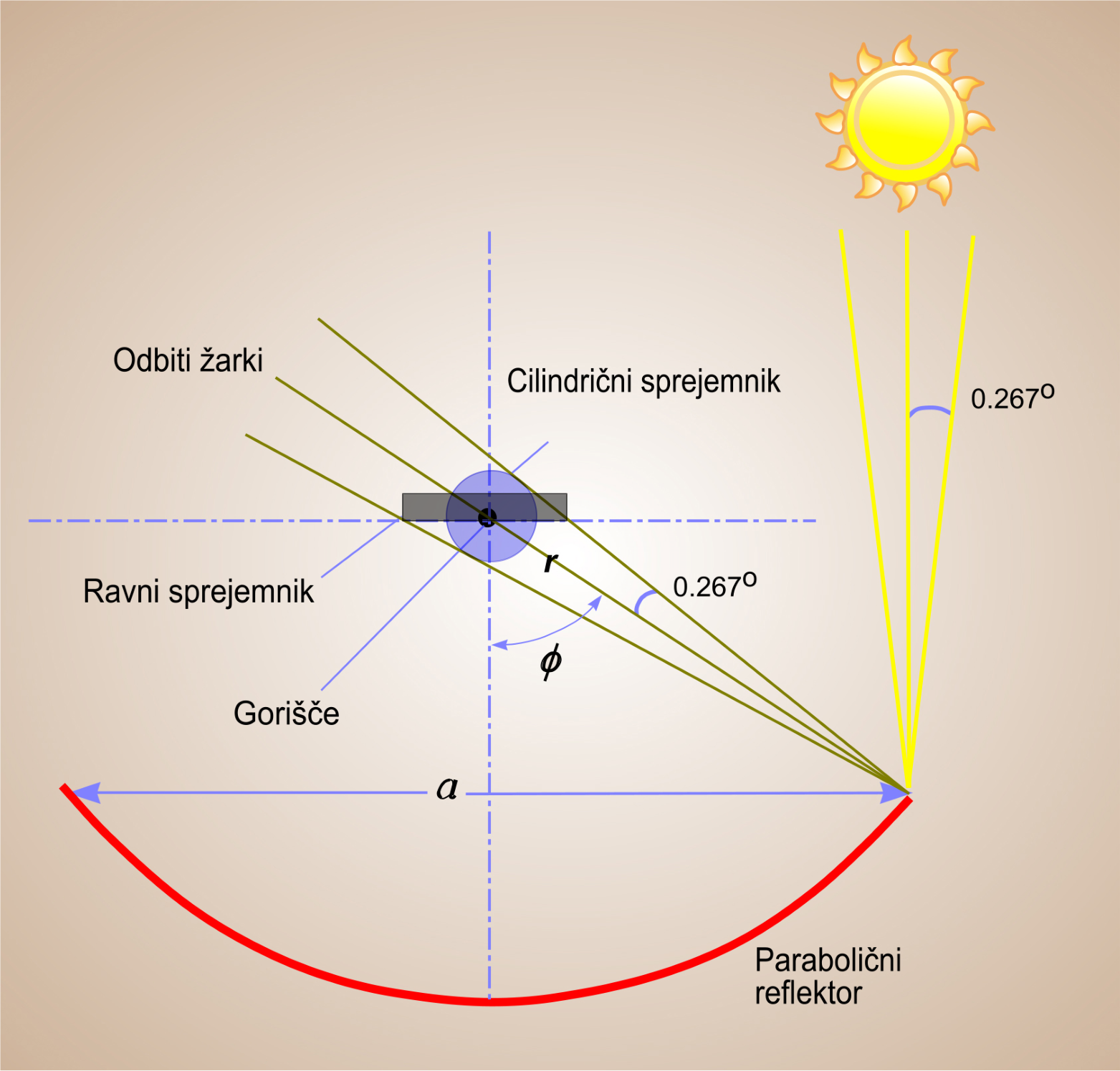
Slika št. 5 - V paraboličnem koncentratorju je odsev žarka za slikanje, odprtina, a. Modra površina posnema položaj valjastega (cevastega) sprejemnika na kontaktni točki. Siva površina posnema ravni sprejemnik na goriščni ravnini. Najmanjšo velikost sprejemnika za prestrezanje vsega odsevnega sevanja je treba ujemati s premerom odsevne grede na goriščni ravnini.

Za linearni sprejemnik se lahko širina slike (W), proizvedene na goriščni ravnini, določi na naslednji način:

Formula W  =

Tukaj predstavljene enačbe lahko uporabimo za oceno velikosti refleksijske svetlobne slike na sprejemniku za različne oblike paraboličnih reflektorjev. Formule vključujejo kot izbrano odprtino reflektorja (širina korita) in (ф) kot merilo parabolične ukrivljenosti. Upoštevajte, da gre za minimalne teoretične dimenzije odsevne slike, ki bi jo izdelalo idealno parabolično ogledalo, ki je popolnoma poravnano. Če pride do pomanjkljivosti na površini zrcala ali pravilnosti kota, se lahko pojavi dodatno širjenje slike.

 Zgoraj opisane geometrijske zasnove se nanašajo na presek paraboličnega reflektorja. V resnici je reflektor sam tridimenzionalen, to je parabolični valj s končno dolžino (l). Torej, stožčasti žarek, ki se odbije v točki na površini paraboličnega reflektorja, bo na goriščni ravnini oblikoval elipso obliko. Vidimo lahko, da se kot refleksijska točka odmakne od vrha proti obodu, se elipse preoblikuje iz krožne v bolj podolgovate oblike (ker bi stožec segal goriščno ravnino z večjim in večjim kotom - slika št. 6.

Če poznamo kotno širino stožca, lahko teoretično izvedemo sliko z dimenzijami elipse in predstavimo kot funkcija ϕ, ki je kot odstopanja od osi parabole. Spodaj so enačbe, ki opisujejo dolžino manjših in glavnih osi elipse.

Manjša os =2rsin(0.2670)

Glavna os = 2r sin(0.2670^o

kjer je razdalja r med fokusom in refleksijsko točko (lokalni radij) na paraboličnem zrcalu (r = f v verigi) in ϕ je kot med osjo parabole in žarkom, 0,267^o kar je pol-kota širine žarkov.

Energijska koncentracija fluksa ~ a / f

Večja zaslonka, pomeni več energije je koncentrirano v določeni velikosti slike. Manjša je žariščna razdalja, manjša je velikost slike, v kateri je koncentracija energije.

Porazdelitev intenzivnosti energijskega toka v koncentrirani sliki ima lahko profil, podoben sliki št. 5, za kvantificiranje tega profila so bili uporabljeni različni modeli.

Na primer, eden od pristopov se imenuje ne enakomerno sončno sevanje čez solarni disk, kar kaže na to, da je sončna svetloba, ki prihaja iz središča sončnega diska, višja od tiste, ki prihaja iz njegovih robov. Brez preveč podrobnih podatkov o tem modelu lahko uporabimo različne diagrame, ki se nanašajo na to tematiko in omogočajo povezovanje različnih parametrov paraboličnega koncentratorja z lokalno intenzivnostjo na sprejemniku.

I.K.